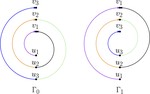
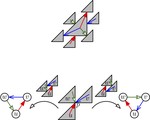
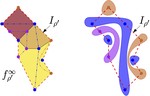
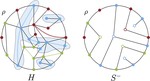
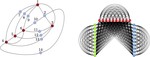
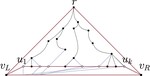
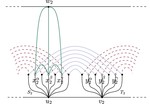
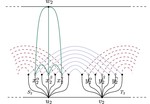
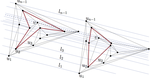
Upward Planar Morphs
We prove that, given two topologically equivalent upward planar straight-line drawings of an $n$-vertex directed graph $G$, there …
Simple k-planar graphs are simple (k + 1)-quasiplanar
A simple topological graph is $k$-quasiplanar ($k\geq 2$) if it contains no $k$ pairwise crossing edges, and $k$-planar if no edge is …
On Planar Greedy Drawings of 3-Connected Planar Graphs
A graph drawing is greedy if, for every ordered pair of vertices $(x,y)$, there is a path from $x$ to $y$ such that the Euclidean …
Extending Upward Planar Graph Drawings
In this paper we study the computational complexity of the Upward Planarity Extension problem, which takes in input an upward planar …
Book Embeddings of Nonplanar Graphs with Small Faces in Few Pages
An embedding of a graph in a book, called book embedding, consists of a linear ordering of its vertices along the spine of the book and …
Beyond level planarity: Cyclic, torus, and simultaneous level planarity
In this paper we settle the computational complexity of two open problems related to the extension of the notion of level planarity to …
Computing k-Modal Embeddings of Planar Digraphs
Given a planar digraph $G$ and a positive even integer $k$, an embedding of $G$ in the plane is $k$-modal, if every vertex of $G$ is …
Reaching 3-Connectivity via Edge-edge Additions
Given a graph $G$ and a pair $\langle e’,e’'\rangle$ of distinct edges of $G$, an edge-edge addition on $\langle …
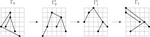
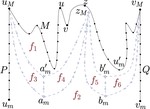
How to Morph a Tree on a Small Grid
In this paper, we study planar morphs between straight-line planar grid drawings of trees. A morph consists of a sequence of morphing …
Extending Upward Planar Graph Drawings
In this paper we study the computational complexity of the Upward Planarity Extension problem, which takes in input an upward planar …
Planarity of Streamed Graphs
In this research we introduce a notion of planarity for graphs that are presented in a streaming fashion. A streamed graph is a stream …
Clustered Planarity with Pipes
In this paper we study the version of the C-Planarity problem in which edges connecting the same pair of clusters must be grouped into …
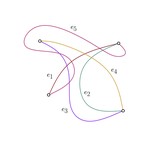
Analogies between the Crossing Number and the Tangle Crossing Number
Tanglegrams are special graphs that consist of a pair of rooted binary trees with the same number of leaves, and a perfect matching …
3-coloring arrangements of line segments with 4 slopes is hard
In a paper first appeared at SODA ’04, Eppstein proved that testing the $3$-colorability of arrangements of line segments is an …
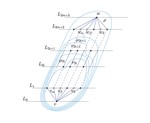
Upward Planar Morphs
We prove that, given two topologically equivalent upward planar straight-line drawings of an $n$-vertex directed graph $G$, there …
Approximation Algorithms for Facial Cycles in Planar Embeddings
Consider the following combinatorial problem$:$ Given a planar graph $G$ and a set of simple cycles $\mathcal C$ in $G$, find a planar …
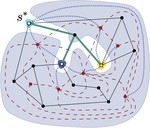
Windrose Planarity: Embedding Graphs with Direction-Constrained Edges
Given a planar graph $G(V,E)$ and a partition of the neighbors of each vertex $v \in V$ in four sets $\overset{\nwarrow}{v}$, …
Algorithms and Bounds for L-Drawings of Directed Graphs
We introduce L-drawings, a novel paradigm for representing directed graphs aiming at combining the readability features of orthogonal …
On Planar Greedy Drawings of 3-Connected Planar Graphs
A graph drawing is greedy if, for every ordered pair of vertices $(x,y)$, there is a path from $x$ to $y$ such that the Euclidean …
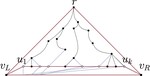
How to Morph Planar Graph Drawings
Given an $n$-vertex graph and two straight-line planar drawings of the graph that have the same faces and the same outer face, we show …
Planar L-Drawings of Directed Graphs
We study planar drawings of directed graphs in the L-drawing standard. We provide necessary conditions for the existence of these …
On the Relationship Between k-Planar and k-Quasi-Planar Graphs
A simple topological graph is $k$-quasiplanar ($k\geq 2$) if it contains no $k$ pairwise crossing edges, and $k$-planar if no edge is …
Square-Contact Representations of Partial 2-Trees and Triconnected Simply-Nested Graphs
A square-contact representation of a planar graph $G=(V,E)$ maps the vertices in $V$ to interior disjoint axis-aligned squares in the …
Strip Planarity Testing for Embedded Planar Graphs
In this paper we introduce and study the Strip Planarity Testing problem, which takes as an input a planar graph $G(V,E)$ and a …
Windrose Planarity: Embedding Graphs with Direction-Constrained Edges
Given a planar graph $G(V,E)$ and a partition of the neighbors of each vertex $v \in V$ in four sets $\overset{\nwarrow}{v}$, …
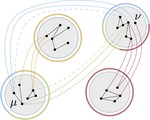
Simultaneous Orthogonal Planarity
We introduce and study the OrthoSEFE-$k$ problem$:$ Given~$k$ planar graphs each with maximum degree 4 and the same vertex set, is …
L-Drawings of Directed Graphs
We introduce L-drawings, a novel paradigm for representing directed graphs aiming at combining the readability features of orthogonal …
Clustered Planarity with Pipes
In this paper we study the version of the C-Planarity problem in which edges connecting the same pair of clusters must be grouped into …
Beyond Level Planarity
In this paper we settle the computational complexity of two open problems related to the extension of the notion of level planarity to …
Planar Graphs with Vertices in Prescribed Regions: models, algorithms, and complexity
The volume and the complexity of structured relational information created and handled by modern information systems has drastically …
Planarity of Streamed Graphs
In this research we introduce a notion of planarity for graphs that are presented in a streaming fashion. A streamed graph is a stream …
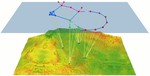
Drawing Georeferenced Graphs - Combining Graph Drawing and Geographic Data
We consider the task of visually exploring relationships (such as established connections, similarity, reachability, etc) among a set …
The Importance of Being Proper - (In Clustered-Level Planarity and T-Level Planarity)
In this paper we study two problems related to the drawing of level graphs, that is, $T$-Level Planarity and Clustered-Level Planarity. …
Relaxing the constraints of clustered planarity
In a drawing of a clustered graph vertices and edges are drawn as points and curves, respectively, while clusters are represented by …
Algorithms and bounds for drawing non-planar graphs with crossing-free subgraphs
We initiate the study of the following problem$:$ Given a non-planar graph $G$ and a planar subgraph $S$ of $G$, does there exist a …
Advancements on SEFE and Partitioned Book Embedding problems
In this work we investigate the complexity of some combinatorial problems related to the Simultaneous Embedding with Fixed Edges (SEFE) …
On Some NP-complete SEFE Problems
In this work we investigate the complexity of some combinatorial problems related to the Simultaneous Embedding with Fixed Edges (SEFE) …
Morphing Planar Graph Drawings Optimally
We provide an algorithm for computing a planar morph between any two planar straight-line drawings of any $n$-vertex plane graph in …
The Importance of Being Proper - (In Clustered-Level Planarity and T-Level Planarity)
In this paper we study two problems related to the drawing of level graphs, that is, $T$-Level Planarity and Clustered-Level Planarity. …
Planar Embeddings with Small and Uniform Faces
Motivated by finding planar embeddings that lead to drawings with favorable aesthetics, we study the problems MINMAXFACE and …
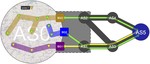
Anchored Drawings of Planar Graphs
In this paper we study the ANCHORED GRAPH DRAWING (AGD) problem$:$ Given a planar graph $G$, an initial placement for its vertices, and …
Strip Planarity Testing
In this paper we introduce and study the strip planarity testing problem, which takes as an input a planar graph $G(V,E)$ and a …
Drawing Non-Planar Graphs with Crossing-Free Subgraphs
We initiate the study of the following problem$:$ Given a non-planar graph $G$ and a planar subgraph $S$ of $G$, does there exist a …